数据透视表的汇总(Aggregator)说白了不就是单元格值范畴上的一个幺半群而已,有什么难以理解的?
—— 笔者对Haskell梗的拙劣模仿
使用数据透视表进行数据统计时,数据源一般有成千上万行的数据,在汇总计算时通过减少对数据源遍历的次数可以显著提升性能。上一文中提到了透视表中引入了在线算法,让我们在计算方差时,可以比竞对少遍历一遍。那对于其他的汇总方式,能否也通过减少对数据源的遍历次数从而提高性能呢?
有,并行算法!(所有的在线算法都能称为并行算法)
数据透视表的本质※
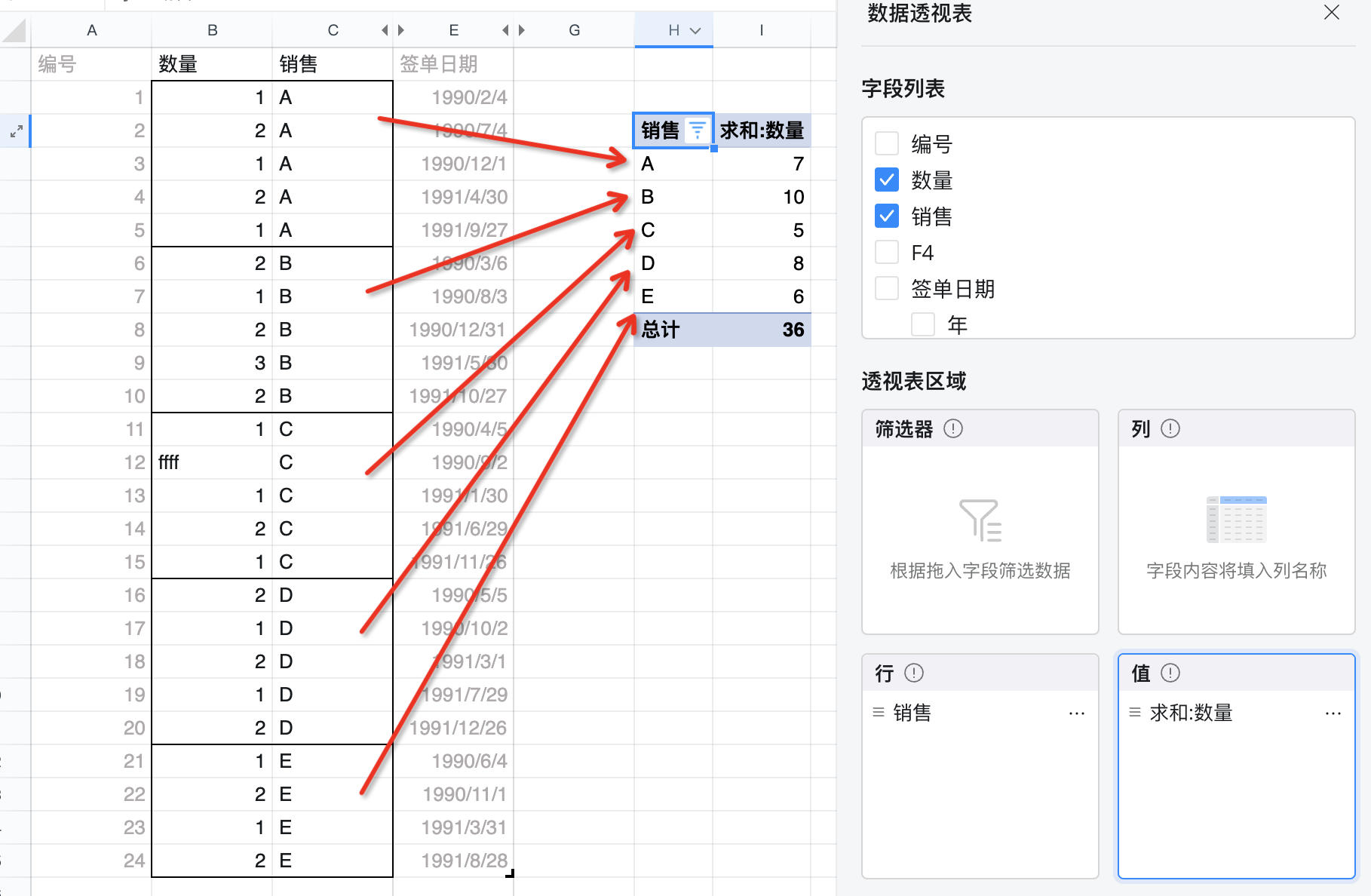
数据透视表作为数据分析工具本质上都是对数据进行「分组」,并对组内数据「汇总」。以下图中左侧销售详情为例,看一下「分组」和「汇总」。
当我们要给老板说明「哪位销售卖了最多东西」时,会把「销售」列作为数据透视表的行,把「数量」作为数据透视表的值。此时,透视表会按照「销售」A~E 的值吧数据源中所有的 23 行数据分为 5 组,并把每组中行的「数量」提取出来,并求和得到 5 个汇总后的数值,分别为 7、10、5、8 和 6。此时就可以得出结论,B 的销售量最多。
汇总如何计算※
如果仅仅是这样,我们可以直接使用 SUMIF 函数就可以分别计算出 A~E 的销售量。然而,作为专业的程序员,我们知道,上面的只是初版需求,老板会继续问你,总销售量是多少?当然,我们可以使用 =SUM(B2:B25) 来计算总量 36,其他的竞品也确实是这样的实现思路。
但是这种思路导致了一个问题:为了计算总量,又把数据源遍历了一遍,这是我们不想要的,因为会让计算的时间几乎翻倍。
这还是只有 1 个分组字段的情况,如果有 2 个字段,需要遍历 4 次;4个字段需要 9 次。N 个字段时需要\((\frac{N}{2}+1)^2\)遍。下图为 4 个字段时需要的 9 次遍历。

如何解决?※
使用公式 =SUM(I4:I9)。直接求和第一阶段的分组汇总结果,即可得出总销量。因为这次参与计算的数据量远小于整个数据源的数据量,耗时四舍五入后耗时只有竞品朴素算法的一半。
这个基于汇总结果再汇总的思路可以直接推广到其他的汇总方式上吗,比如均值?
答案是否定的,并不可以。因为均值的均值不是真正的均值。以下图为例,F2 这一列的 7 个数字的均值是 1.43,但是对 A 和 B 的结果求均值时 1.5。

透视表汇总的并行算法※
均值的中间结果※
上面基于汇总结果再汇总的思路大体方向没错,只是均值作为结果并不支持再次汇总,但我们可以找到一个计算均值过程中支持汇总的中间结果,是包含求和与计数的结构体:
{
sum: number;
cnt: number;
}此时,A 组的中间结果是 { sum: 6, cnt: 3 },B 组的中间结果是 { sum: 4, cnt: 4 }
分组 | 初始结果 | 中间结果 | 最终结果 \(sum\div{cnt}\) |
A | { sum: 0, cnt: 0 } | { sum: 6, cnt:3 } | 2 |
B | { sum: 0, cnt: 0 } | { sum: 4, cnt:4 } | 1 |
总计 | { sum: 0, cnt: 0 } | {sum: 6+4, cnt: 3+4} | 1.43... |
自此,透视表计算均值的算法的结果已经可以支持再次汇总,具备了遍历一遍即可求出均值的能力。均值汇总器(Aggregator)的代码如下:
class AverageAggregator extends Aggregator {
private readonly sum: number = 0;
private readonly cnt: number = 0;
map(val: number) {
return { sum: val, cnt:1 };
}
reduce(val: number) {
const element = this.map(val);
this.sum += v.sum;
this.cnt += v.cnt;
}
getValue() {
const { sum, cnt } = this;
return cnt === 0 ? 0 : sum/cnt;
}
}数学抽象※
数据透视表除了均值,还有很多其他的汇总方式,比如最大最小值、方差,上述算法能否起效?甚至更进一步,能否让用户按照我们的规则去实现自定义汇总算法?
答案是肯定的,只要我们能够对透视表的汇总算法做一个抽象。
并行算法是幺半群※
上面提到的算法便是均值的并行算法,特点是将数据分块独立处理后将结果汇总的算法。独立处理意味着相互之前没有依赖关系,这是结合律的体现。讲到这里,相信学过离散数学的同学一眼就能看出 AvgAggergator 是一个幺半群。
半群※
有非空集合\(S\),在\(S\)上定义了二元运算\(\circ\):\(S\times{S} \rightarrow S\) (\(\langle S,\circ \rangle\)称为广群)。若运算\(\circ\)满足结合律,即:
\(\forall a,b,c \in S\) 有 \((a\circ b)\circ c = a \circ (b \circ c)\)
则称\(\langle S,\circ \rangle\)为半群。
上面用于计算均值的 AverageAggergator 中 reduce 方法就是二元运算。
幺半群※
有幺元的半群是幺半群。
幺元※
集合 \(S\) 中一个独特的元素 \(e\),\(e\)与集合中任意的其他元素 \(a\) 做 \(e \circ a\) 和运算 \(a \circ e\),结果都是 \(a\),则称 \(e\) 为单位元或者幺元。整数乘法就是一个幺半群,其幺元为 1。
显然,下表的「初始结果」就是幺元。

推广到其他汇总器※
对于其他的汇总器,只要「运算满足结合律且找到幺元」就可以享受到并行汇总的红利——不管透视表有基层汇总,只需要一次遍历就能计算出所有结果。
以最大值最小值和最小公倍数为例
要素 | 最大值 | 最小值 | 最小公倍数 |
运算 | Math.max(a, b) | Math.min(a, b) | lcm(a, b) |
幺元 | Number.MIN_VALUE | Number.MAX_VALUE | 1 |
总结※
- 使用并行算法可以让透视表一次遍历就能计算出所有结果。除了在透视表中的应用,因为半群中「结合律」的特性,并行算法(在线算法)可以在各种高性能计算领域发光发热(由半群演化出来的迹幺半群和历史幺半群是进程演算和并行计算的基础)。
- 透视表中的汇总器(Aggregator)说白了不就是单元格值范畴上的一个幺半群而已,是不是很好理解了。
