对于中学生来说有点幼稚,但对于成年人来说刚刚好
人列计算机※
《三体》中牛顿和冯·诺依曼说服秦始皇用三千万秦兵组成「人列计算机」来计算三颗恒星的运动轨迹。
今天我们也来组两台人列计算机,站在 CPU 的视角上看在线算法在一些场合的优势。

在线算法和离线算法※
在线算法是一种处理输入数据的独特形式,其计算过程中并不要求所有输入数据在算法开始运行时即完备,反而可对逐步输入的资料加以处理并在输入完最后一项资料之后输出运算结果。与之相对的成为离线算法,则假设输入数据在计算开始前已完备。
一般在数据已经完备的情况下,离线算法比在线算法的性能好。而且离线算法不一定有对应的在线算法。
—— Online Algorithm 维基百科
很多我们熟悉的离线算法,比如插入排序、贪心算法、感知器以及今天我们「人列计算机」要运行的方差算法。
方差的计算方法※
方差(Variance)是描述随机变量的离散程度的度量,直观上看是一组数字与其均值之间距离,在概率论和统计学中占据非常核心的地位。在 AI 领域中模型评估、特征选择、数据预处理等方面也都有方差的身影。
其计算公式为 \(Variance = \frac{\sum_{i=1}^{n}(x_i-\bar{x}^2)}{n}\)。对于下面的 6 个数,很显然😏方差是10。
| 95 | 98 | 99 | 101 | 102 | 105 |
朴素的离线算法※
我们一起复习下在中学阶段根据方差的定义给出的计算方法:
- 遍历一遍所有数,相加得到总和 \(sum\),并顺便计算数字的个数 \(cnt\);
- 使用 \(sum/cnt\) 求出均值 \(avg\);
- 再遍历一遍所有数,依次计算每个数与均值的距离(差的平方和)\(\sum_{i=1}^{n}(x_i-\bar{x})^2\);
- 除以个数 \(cnt\),得出方差。
方差的在线算法※
将方差的公式运用初中的数学知识化简后即可得到在线算法用到的公式,我们一起来化简一下:
\(Variance = \frac{\sum_{i=1}^{n}(x_i-\bar{x}^2)}{n}\)
\(=\frac{(x_1-\bar{x})^2+(x_2-\bar{x})^2+...+(x_n-\bar{x})^2}{n}\)
\(=\frac{(x_1^2-2x_1\bar{x}+\bar{x}^2)+(x_2^2-2x_22\bar{x}+\bar{x}^2)+...+(x_n^2-2x_n\bar{x}+\bar{x}^2)}{n}\) // 分子中各项展开
\(=\frac{x_1^2+x_2^2+...+x_n^2}{n} - \frac{2x_1\bar{x}+2x_2\bar{x}+...+2x_n\bar{x}}{n} + \frac{\bar{x}^2+\bar{x}^2+...+\bar{x}^2 }{n}\) // 分子中各项的前中后分成 3 组
\(=\frac{x_1^2+x_2^2+...+x_n^2}{n} - 2\bar{x}\frac{x_1+x_2+...+x_n}{n} + \frac{\bar{x}^2+\bar{x}^2+...+\bar{x}^2 }{n}\)// 对中间组提取公因式 \(2\bar{x}\)
\(=\frac{x_1^2+x_2^2+...+x_n^2}{n} - 2\bar{x}\bar{x} + \bar{x}^2\) // 中间组\(\frac{x_1+x_2+...+x_n}{n}\)即均值\(\bar{x}\),后组上下约掉\(n\)
\(=\frac{ssq}{n} - \bar{x}^2\) // 平方和记为 \(ssq=x_1^2+x_2^2+...+x_n^2\)
至此,我们得出了另一种方差的计算方式,其过程是:
- 遍历所有的数,依次计算每个数的和 \(sum\)、平方和 \(ssq\)、个数 \(cnt\);
- 根据公式 \(\frac{ssq}{cnt}-(sum/cnt)^2\) 得出方差。
比较离线算法和在线算法的步骤,可以看出相较于离线算法的两次遍历,在线算法只需要一次遍历即可得出结果。
人列计算机 PK 游戏※
两台人列计算机※
上面方差的离线算法和在线算法已经确定,相信大家对于两种算法的步骤已了然于心。现在我们挑选现场 10 位同学组两个人列计算机,分别用上面的在线和离线算法计算方差。
运行的程序-计算令牌※
程序算法※
- 有 1 人作为裁判,负责下令开始并统计计算两组的耗时;
- 10 人分为 A、B 两组,组成人列计算机;
- 每人手持一个数字(Input Number),当拿到计算令牌时可以计算:按照本组的算法把需要计算的结果填写到计算令牌上,并传给同组的下一位同学;
Input Number 第 1 人 4 第 2 人 6 第 3 人 2 第 4 人 8 - 如果计算令牌上的数据足够计算出最终的方差结果时,举手并给出结果,裁判记录该组耗时。
胜负判定※
耗时最短的组获胜。
代码中的实际表现※
| 少量数据 | 大量数据 | |
| jsbench | https://jsben.ch/FSgwv | https://jsben.ch/gCpbF |
| 结果 | 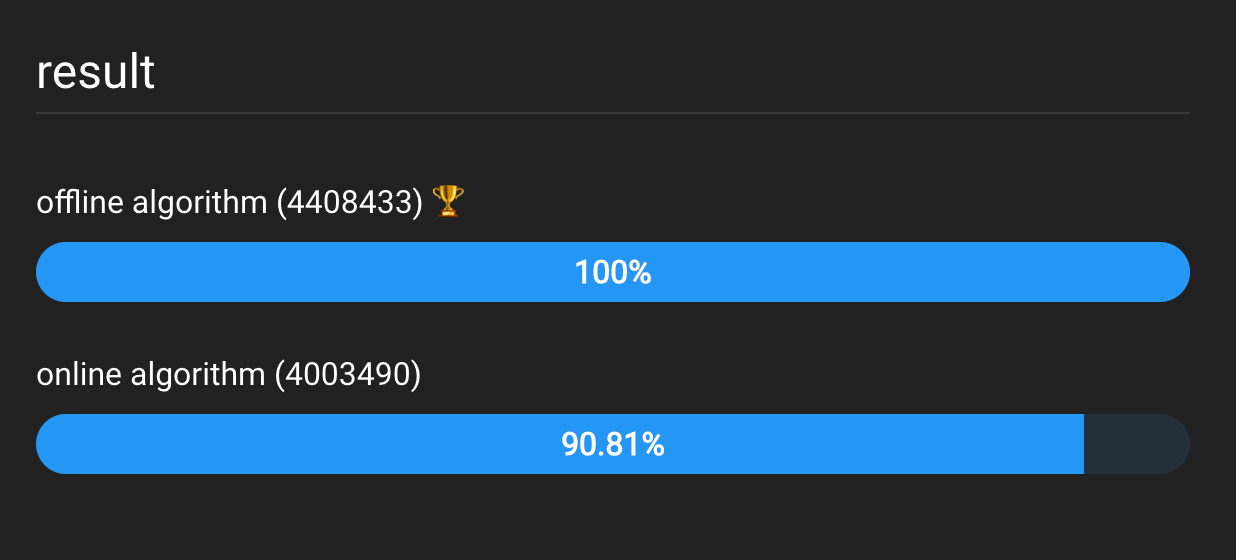 | 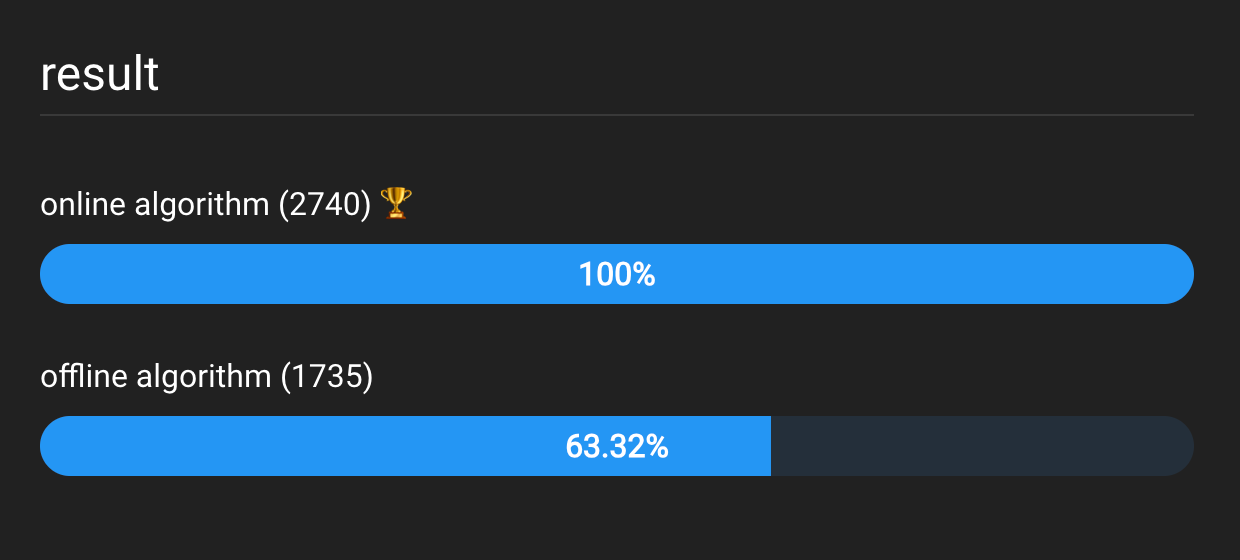 |
| 解读 | 数据量小时,离线算法有优势 | 数据量大时,在线算法有优势 |
游戏总结※
- 在线算法可以流式地处理输入的数据,在处理实时数据、海量数据时有良好的表现;
- 彩排和分享现场该游戏都是在线算法获胜。因为数据读取成本越高,在线算法的一次遍历优势就越大。
在线算法的应用※
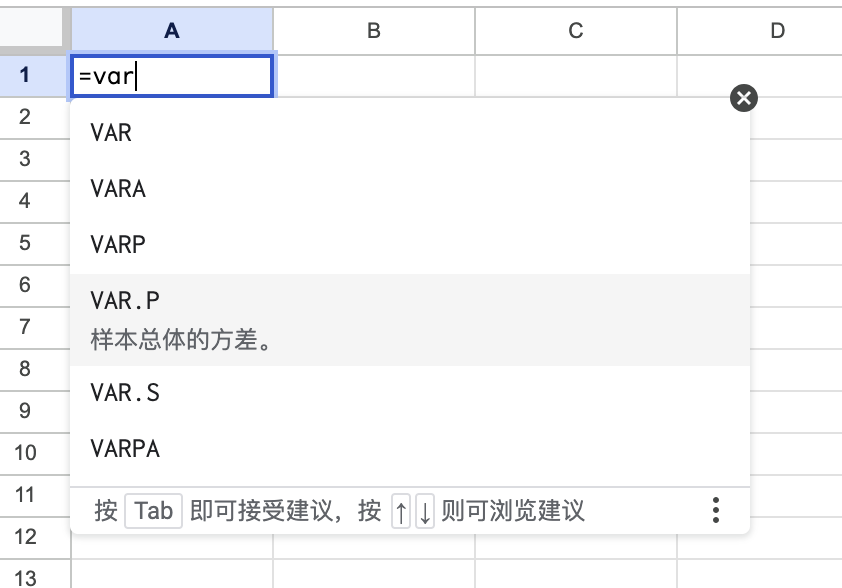
表格公式中※
以 Var 开头的多个公式都是与方差计算有关的,业内的在线表格根据需求的不同在线算法和离线算法都有使用。
数据透视表中※
数据透视表是表格中的重要功能,其中值的计算方式有十几种,其中 4 个是跟方差相关的,业内的表格也是采取了不同的实现方式:
- AntV 的 DataSet 和某 S 表格、某 T 表格等在线表格竞品使用了离线算法;
- 某商业控件使用了上面提到的在线算法;
- 笔者在实现数据透视表时使用了上面在线算法的变种「并行化的 Welford 算法」。
其他领域※
人工智能领域中的 PyTorch 和 Nvdia apex 中计算方差也使用的是 Welford 在线算法。
- PyTorch SharedReduceOps.h
- Nvidia apex cuda_kernel.cu
扩展阅读※
问:我们推导的在线算法有什么问题,为什么使用的是 Welford 在线算法?
答:算法的准确性永远优先于计算速度。上面我们推导的在线算法虽然在数学上没有问题,且有一部分厂商也在使用,但其实由于计算机的浮点误差积累效应,这种平方和在线算法与实际的结果可能会大相径庭,详细可以参阅 JD·库克 关于这个场景的分享。好在上世纪六十年代已经有数学家解决了该问题,Welford 方差在线算法既能达到在线算法一次遍历的效果,又能兼顾浮点误差。
